Bootstrapping Regression Coefficients in grouped data using Tidymodels

Load libraries

library(tidyverse)
library(tidymodels)
library(rstatix)
library(ggpubr)

Load data

Again, I’ll use the iris data set in this post to keep things simple.

data(iris)

Simple Linear Regression

As we have seen in the previous post that sepal and petal lengths are positively related to each other. This means that if sepal length increases, petal length also increases, despite the fact of iris species.

iris %>% 
  ggplot(aes(x = Sepal.Length, y = Petal.Length)) +
  geom_point(colour = "orange", alpha = 0.6) +
  geom_smooth(method = "lm") +
  stat_cor(method = "pearson", cor.coef.name = "r", p.accuracy = 0.001, r.accuracy = 0.01) +
  labs(x = "Sepal length", y = "Petal length") +
  theme_bw()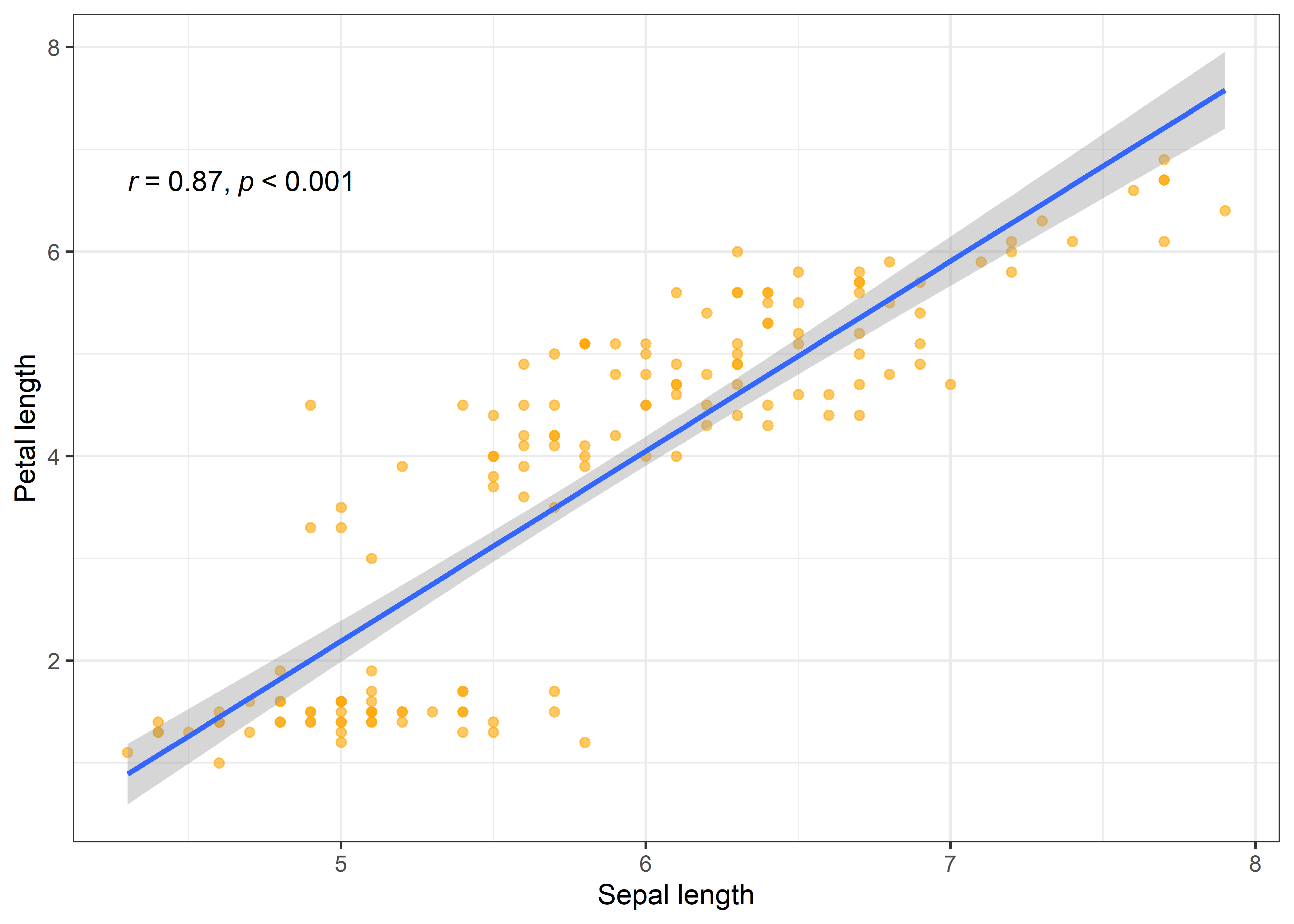

Now, I’ll run the regression analysis between sepal and petal length for each iris species separately. First, I’ll nest the species and then use purrr::map() inside mutate function to run the regression analysis in nest'ed data. This is the speciality of thetidymodels` workflow to design complex analyses in one sequence.

Regression analysis by groups (Species)

point <- iris %>%
  nest(data = -c(Species)) %>% 
  mutate(model = map(data, ~lm(Sepal.Length ~ Petal.Length, data = .x)), 
         coefs = map(model, tidy)) %>% 
  unnest(coefs) %>% 
  select(-data, -model)

point

## # A tibble: 6 × 6
##   Species    term         estimate std.error statistic  p.value
##   <fct>      <chr>           <dbl>     <dbl>     <dbl>    <dbl>
## 1 setosa     (Intercept)     4.21     0.416      10.1  1.61e-13
## 2 setosa     Petal.Length    0.542    0.282       1.92 6.07e- 2
## 3 versicolor (Intercept)     2.41     0.446       5.39 2.08e- 6
## 4 versicolor Petal.Length    0.828    0.104       7.95 2.59e-10
## 5 virginica  (Intercept)     1.06     0.467       2.27 2.77e- 2
## 6 virginica  Petal.Length    0.996    0.0837     11.9  6.30e-16

Here, the term indicates Intercept and slope coefficients of Petal length and in each iris species. The estimates can be found in the estimate column. The tidy format provides results in tibble format that can be easily used for further wrangling and data visualizations using ggplot2 package and related libraries.

iris %>% 
  ggplot(aes(x = Sepal.Length, y = Petal.Length, color = Species)) +
  geom_point() +
  geom_smooth(method = "lm") +
  stat_cor(method = "pearson", cor.coef.name = "r", p.accuracy = 0.001, r.accuracy = 0.01) +
  labs(x = "Sepal length", y = "Petal length") +
  theme_test()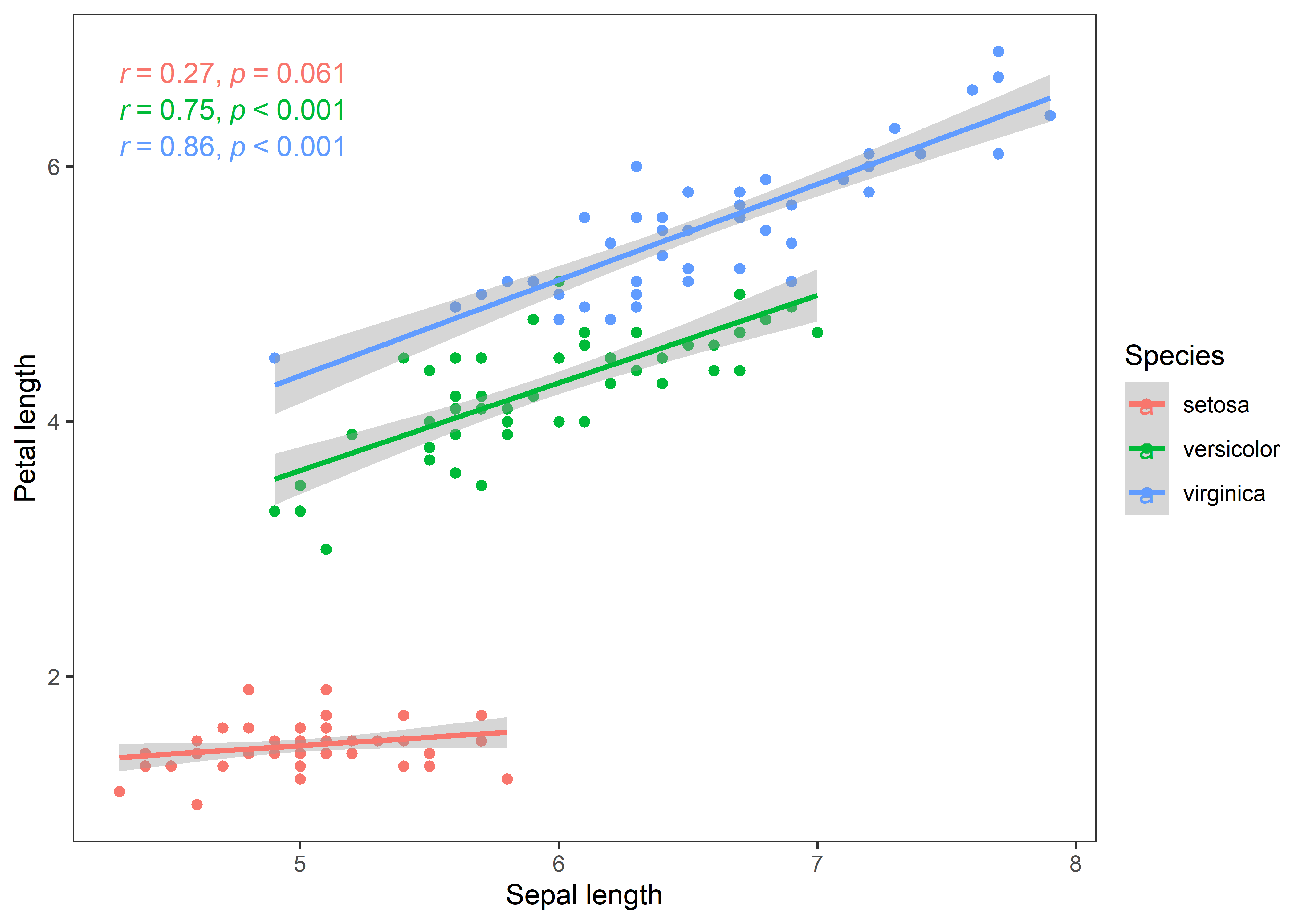

The curves depict a clear story of the associations in all iris species. Now, I’ll bootstrap regression (slope) estimates to test how robust are the beta coefficients of regression between sepal and petal length in iris species.

Bootsrapped Regression

I’ll nest the data by species as we want bootstrapped estimates for all iris species. After that, I’ll define the bootstraps for each nested tibble using the bootstraps function inside purrr::map(). Then I’ll perform the regression analysis on each bootstrapped tibble (splits). Finally, I’ll unnest the tidied data frames so we can see the results in a flat tibble.

boot_reg <- iris %>% 
  nest(data = -c(Species)) %>% # grouping the species
  mutate(boots = map(data, ~bootstraps(.x, times = 1000, apparent = FALSE))) %>% # defining bootstraps
  unnest(boots) %>% # un-nesting bootstrapped data lists
  mutate(model = map(splits, ~lm(Sepal.Length ~ Petal.Length, data = analysis((.)))), 
         coefs = map(model, tidy)) # performing regression
  
reg <- boot_reg %>% 
  unnest(coefs) %>% # unnesting tidied data frames
  select(-data, -splits, -id, -model)

reg

## # A tibble: 6,000 × 6
##    Species term         estimate std.error statistic  p.value
##    <fct>   <chr>           <dbl>     <dbl>     <dbl>    <dbl>
##  1 setosa  (Intercept)    4.15       0.393    10.6   3.99e-14
##  2 setosa  Petal.Length   0.580      0.262     2.21  3.19e- 2
##  3 setosa  (Intercept)    3.80       0.491     7.73  5.61e-10
##  4 setosa  Petal.Length   0.862      0.341     2.53  1.49e- 2
##  5 setosa  (Intercept)    4.99       0.394    12.7   6.34e-17
##  6 setosa  Petal.Length   0.0558     0.267     0.209 8.36e- 1
##  7 setosa  (Intercept)    4.33       0.257    16.8   8.66e-22
##  8 setosa  Petal.Length   0.486      0.174     2.80  7.38e- 3
##  9 setosa  (Intercept)    4.72       0.436    10.8   1.76e-14
## 10 setosa  Petal.Length   0.180      0.297     0.604 5.49e- 1
## # … with 5,990 more rows
## # ℹ Use `print(n = ...)` to see more rows

Visualizing the bootstrapped estimates

One of the simple ways to visualize bootstrapped estimates is to draw the distributions along with observed estimates, i.e., estimates from raw data and confidence intervals, e.g. 95%.

Distributions

# confidence interval
CI <- reg %>%
  filter(term == "Petal.Length") %>% 
  group_by(Species) %>%
        summarise(lwr_CI = quantile(estimate, 0.025),
                  .estimate = median(estimate),
                  upr_CI = quantile(estimate, 0.975))

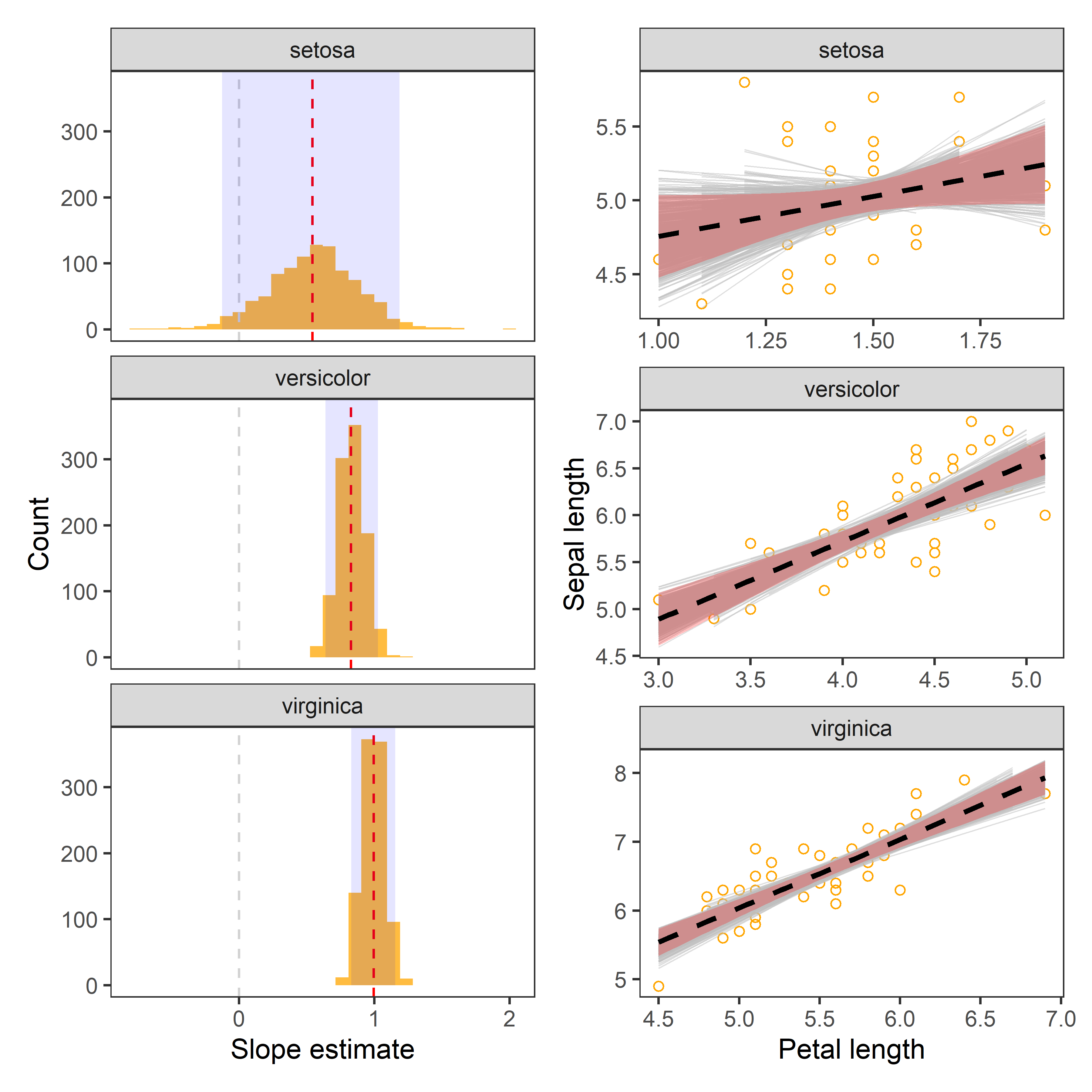
reg %>%
  filter(term == "Petal.Length") %>%
  ggplot(aes(x = estimate)) +
  geom_histogram(bins = 30, fill = "orange", alpha = 0.75) +
  geom_vline(aes(xintercept = 0), col = "lightgrey", lty = 2, size = 0.5) +
  geom_vline(aes(xintercept = estimate), data = point %>% filter(term == "Petal.Length"), lty = 2, col = "red") +
  geom_rect(aes(x = .estimate, xmin = lwr_CI, xmax = upr_CI, ymin = 0, ymax = Inf), data = CI, alpha = 0.1, fill = "blue") +
  labs(x = "Slope estimate", y = "Count") +
  theme_test() +
  facet_wrap(~Species)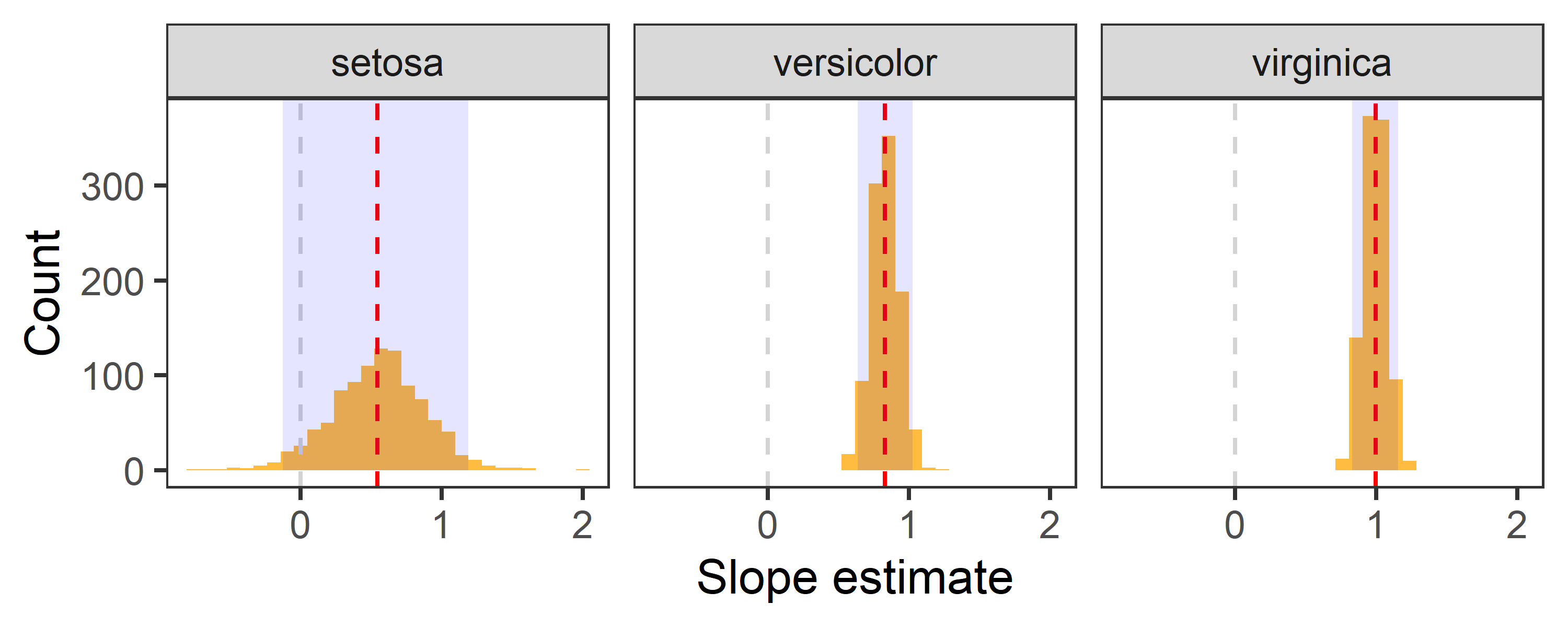

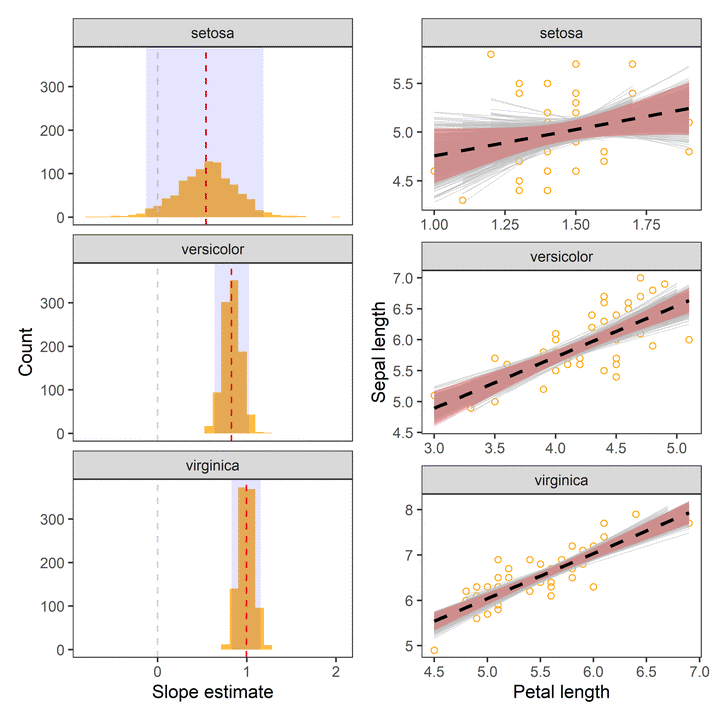
• Red dashed line indicates the point estimate of regression slopes.
• Grey dashed line indicates 0, i.e., no change.
• The shaded area indicates 95% confidence interval.

Possible model fits

Now, I’ll use augment function to extract fitted data from each bootstrapped split in each iris species. We can then use this data to visualize the uncertainty in the fitted curve.

boot_aug <- 
  boot_reg %>% 
  mutate(augmented = map(model, augment)) %>% 
  unnest(augmented)

boot_aug

## # A tibble: 150,000 × 14
##    Species data     splits          id    model coefs    Sepal…¹ Petal…² .fitted
##    <fct>   <list>   <list>          <chr> <lis> <list>     <dbl>   <dbl>   <dbl>
##  1 setosa  <tibble> <split [50/19]> Boot… <lm>  <tibble>     4.8     1.6    5.08
##  2 setosa  <tibble> <split [50/19]> Boot… <lm>  <tibble>     5.2     1.5    5.02
##  3 setosa  <tibble> <split [50/19]> Boot… <lm>  <tibble>     5.1     1.7    5.14
##  4 setosa  <tibble> <split [50/19]> Boot… <lm>  <tibble>     5       1.4    4.96
##  5 setosa  <tibble> <split [50/19]> Boot… <lm>  <tibble>     5.2     1.5    5.02
##  6 setosa  <tibble> <split [50/19]> Boot… <lm>  <tibble>     5       1.6    5.08
##  7 setosa  <tibble> <split [50/19]> Boot… <lm>  <tibble>     4.5     1.3    4.91
##  8 setosa  <tibble> <split [50/19]> Boot… <lm>  <tibble>     4.8     1.6    5.08
##  9 setosa  <tibble> <split [50/19]> Boot… <lm>  <tibble>     5.4     1.7    5.14
## 10 setosa  <tibble> <split [50/19]> Boot… <lm>  <tibble>     5.4     1.5    5.02
## # … with 149,990 more rows, 5 more variables: .resid <dbl>, .hat <dbl>,
## #   .sigma <dbl>, .cooksd <dbl>, .std.resid <dbl>, and abbreviated variable
## #   names ¹​Sepal.Length, ²​Petal.Length
## # ℹ Use `print(n = ...)` to see more rows, and `colnames()` to see all variable names

Note: See the number of rows in the extracted data. This is the data of 1000 bootstrapped fits.

Uncertainty in Fitted curve

boot_aug %>%
  ggplot(aes(x = Petal.Length, y = Sepal.Length)) +
  geom_point(colour = "orange", alpha = 0.5, shape = 1) +
  geom_line(aes(y = .fitted, group = id), col = "grey", alpha = 0.5, size = 0.25) +
  geom_smooth(aes(x = Petal.Length, y = Sepal.Length), data = iris, method = "lm",colour = "black", linetype = "dashed", fill = "red", alpha = 0.25) +
  labs(x = "Petal length", y = "Sepal length") +
  facet_wrap(~ Species, scales = "free") +
  theme_test()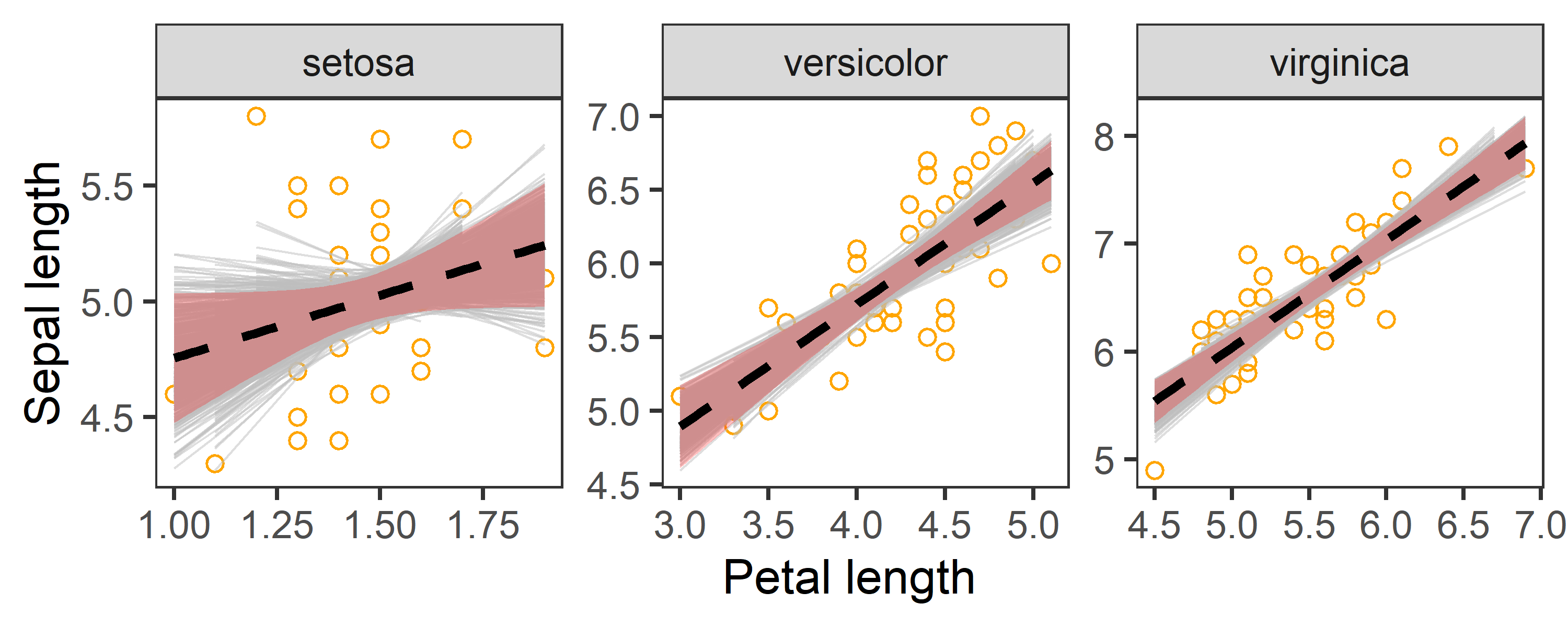

In the above charts:

• Dashed line represents the observed slope of regression between Petal and Sepal length.
• Shaded red area represents 95% confidence interval for the observed slope.
• Grey lines are 1000 bootstrapped fits.

The chart indicates that our estimates of regression coefficients are robust.

That’s it!

Feel free to reach me out if you got any questions.